轉貼:https://www.hksilicon.com/articles/1732695
聚類算法是機器學習中涉及對數據進行分組的一種算法。在給定的數據集中,我們可以通過聚類算法將其分成一些不同的組。在理論上,相同的組的數據之間有相同的屬性或者是特徵,不同組數據之間的屬性或者特徵相差就會比較大。聚類算法是一種非監督學習算法,並且作為一種常用的數據分析算法在很多領域上得到應用。
在數據科學領域,我們利用聚類分析,通過將數據分組可以比較清晰的獲取到數據信息。今天我們來看看,作為數據科學家需要知道並掌握的五種比較比較流行的聚類算法。
K-means 聚類算法
K-means 聚類算法 可能是大家最為熟悉的聚類算法。它在許多的工業級數據科學和機器學習課程中都有被講解。並且容易理解和實現相應功能的代碼 。 比如以下的圖片:
 k-means聚類
k-means聚類
-
首先,我們確定要聚類的數量,並隨機初始化它們各自的中心點。為了確定要聚類的數量,最好快速查看數據並嘗試識別任何不同的分組。中心點是與每個數據點向量長度相同的向量,是上圖中的「x」。
-
通過計算當前點與每個組中心之間的距離,對每個數據點進行分類,然後歸到與距離最近的中心的組中。
-
基於迭代后的結果,計算每一類內,所有點的平均值,作為新簇中心。
-
迭代重複這些步驟,或者直到組中心在迭代之間變化不大。您還可以選擇隨機初始化組中心幾次,然後選擇看起來提供最佳結果。
k-means的優點是速度非常快,因為我們真正要做的就是計算點和組中心之間的距離;計算量少!因此,它具有線性複雜性o(n)。
另一方面,k-means有兩個缺點。首先,您必須先確定聚類的簇數量。理想情況下,對於一個聚類算法,我們希望它能幫我們解決這些問題,因為它的目的是從數據中獲得一些洞察力。k-均值也從隨機選擇聚類中心開始,因此它可能在算法的不同運行中產生不同的聚類結果。因此,結果可能不可重複,缺乏一致性。
K中位數是與K均值相關的另一種聚類算法,除了不使用平均值重新計算組中心點之外,我們使用組的中位數向量。這種方法對異常偏離值不太敏感(因為使用了中值),但對於較大的數據集來說要慢得多,因為在計算中值向量時,每次迭代都需要排序。
首先,我們確定要聚類的數量,並隨機初始化它們各自的中心點。為了確定要聚類的數量,最好快速查看數據並嘗試識別任何不同的分組。中心點是與每個數據點向量長度相同的向量,是上圖中的「x」。
通過計算當前點與每個組中心之間的距離,對每個數據點進行分類,然後歸到與距離最近的中心的組中。
基於迭代后的結果,計算每一類內,所有點的平均值,作為新簇中心。
迭代重複這些步驟,或者直到組中心在迭代之間變化不大。您還可以選擇隨機初始化組中心幾次,然後選擇看起來提供最佳結果。
Mean-Shift 聚類
Mean-shift 聚類是一個基於滑窗的算法,嘗試找到數據點密集的區域。它是一個基於質心的算法,也就是說他的目標是通過更新中心點候選者定位每個組或類的中心點,將中心點候選者更新為滑窗內點的均值。這些候選滑窗之後會在後處理階段被過濾,來減少臨近的重複點,最後形成了中心點的集合和他們對應的組。查看下面的說明圖。
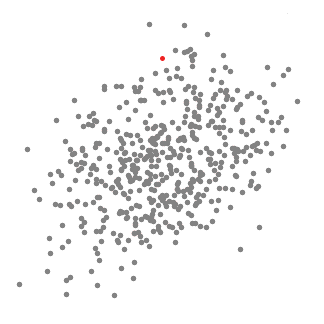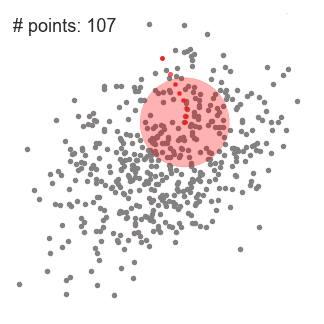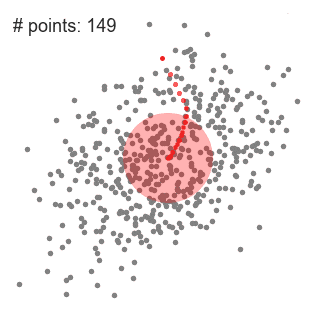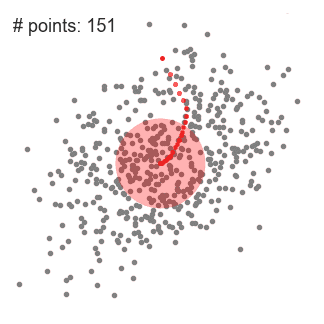 單滑窗的 Mean-Shift 聚類
單滑窗的 Mean-Shift 聚類
-
為了解釋 mean-shift,我們將考慮一個二維空間中的點集,像上圖所示那樣。我們以一個圓心在C點(隨機選擇)的圓形滑窗開始,以半徑 r 作為核。Mean shift 是一個爬山算法,它每一步都迭代地把核移動到更高密度的區域,直到收斂位置。
-
在每次迭代時,通過移動中心點到滑窗中點的均值處,將滑窗移動到密度更高的區域(這也是這種算法名字的由來)。滑窗內的密度與在其內部點的數量成正比。很自然地,通過將中心移動到窗內點的均值處,可以逐步的移向有個高的密度的區域。
-
我們繼續根據均值來移動滑窗,直到有沒有哪個方向可以使核中容納更多的點。查看上面的圖,我們一直移動圓圈直到密度不再增長。(即窗內點的數量不再增長)。
-
用很多滑窗重複1-3這個過程,直到所有的點都包含在了窗內。當多個滑動窗口重疊時,包含最多點的窗口將被保留。然後,根據數據點所在的滑動窗口對數據點進行聚類。
 Mean-Shift 聚類的全部過程
與 K-means 聚類不同的是,Mean-Shift 不需要選擇聚類的數量,因為mean-shift 自動發現它。這是一個很大的優點。事實上聚類中心向著有最大密度的點收斂也是我們非常想要的,因為這很容易理解並且很適合於自然的數據驅動的場景。缺點是滑窗尺寸/半徑「r「的選擇需要仔細考慮。
Mean-Shift 聚類的全部過程
與 K-means 聚類不同的是,Mean-Shift 不需要選擇聚類的數量,因為mean-shift 自動發現它。這是一個很大的優點。事實上聚類中心向著有最大密度的點收斂也是我們非常想要的,因為這很容易理解並且很適合於自然的數據驅動的場景。缺點是滑窗尺寸/半徑「r「的選擇需要仔細考慮。
- 為了解釋 mean-shift,我們將考慮一個二維空間中的點集,像上圖所示那樣。我們以一個圓心在C點(隨機選擇)的圓形滑窗開始,以半徑 r 作為核。Mean shift 是一個爬山算法,它每一步都迭代地把核移動到更高密度的區域,直到收斂位置。
- 在每次迭代時,通過移動中心點到滑窗中點的均值處,將滑窗移動到密度更高的區域(這也是這種算法名字的由來)。滑窗內的密度與在其內部點的數量成正比。很自然地,通過將中心移動到窗內點的均值處,可以逐步的移向有個高的密度的區域。
- 我們繼續根據均值來移動滑窗,直到有沒有哪個方向可以使核中容納更多的點。查看上面的圖,我們一直移動圓圈直到密度不再增長。(即窗內點的數量不再增長)。
- 用很多滑窗重複1-3這個過程,直到所有的點都包含在了窗內。當多個滑動窗口重疊時,包含最多點的窗口將被保留。然後,根據數據點所在的滑動窗口對數據點進行聚類。
基於密度的帶噪聲的空間聚類的應用(DBSCAN)
DBSCAN 是一個基於密度的聚類算法,與 mean-shift 相似,但是有幾個值得注意的優點。查看下面這個花哨的圖片,我們開始吧!
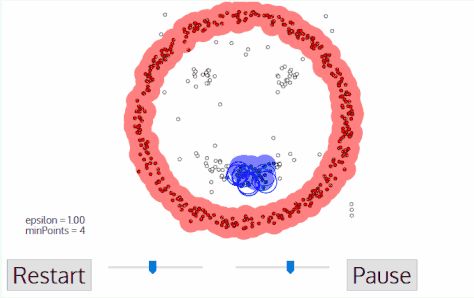 DBSCAN 笑臉聚類
DBSCAN 笑臉聚類
-
DBSCAN 從一個任意的還沒有被訪問過的啟動數據點開始。用一個距離 epsilon ε 將這個點的鄰域提取出來(所有再距離 ε 內的點都視為鄰居點)。
-
如果在鄰域內有足夠數量的點(根據 minPoints) ,那麼聚類過程開始,並且當前數據點變成新集群中的第一個點。否則,該點將被標記為噪聲(之後這個噪聲點可能會變成集群中的一部分)。在這兩種情況中的點都被標記為」已訪問「。
-
對於這個新集群中的第一個點,在它 ε 距離鄰域內的點已將變成相同集群中的一部分。這個讓所有在 ε 鄰域內的點都屬於相同集群的過程在之後會一直被重複做,直到所有新點都被加進集群分組中。
-
第 2,3 步的過程會一直重複直到集群內所有點都被確定,即所有在 ε 鄰域內的點都被訪問且被打上標籤。
-
一旦我們在當前集群做完這些,一個新的未被訪問的點會被提取並處理,從而會接着發現下一個集群或噪聲。這個過程反覆進行直到所有的點都被編輯為已訪問。既然在最後所有的點都被訪問,那麼每個點都被標記為屬於一個集群或者是噪聲。
相較於其他聚類算法,DBSCAN 提出了一些很棒的優點。首先,它根本不需要預置集群的數量。它還將離群值認定為噪聲,不像 mean-shift 中僅僅是將它們扔到一個集群里,甚至即使該數據點的差異性很大也這麼做。另外,這個算法還可以很好的找到任意尺寸核任意形狀的集群。
SBSCAN 最大的缺點是當集群的密度變化時,它表現的不像其他算法那樣好。這是因為當密度變化時,距離的閾值 ε 和用於確定鄰居點的 minPoints 也將會隨之改變。這個缺點也會發生在很高為的數據中,因為距離閾值 ε 變得很難被估計。
DBSCAN 從一個任意的還沒有被訪問過的啟動數據點開始。用一個距離 epsilon ε 將這個點的鄰域提取出來(所有再距離 ε 內的點都視為鄰居點)。
如果在鄰域內有足夠數量的點(根據 minPoints) ,那麼聚類過程開始,並且當前數據點變成新集群中的第一個點。否則,該點將被標記為噪聲(之後這個噪聲點可能會變成集群中的一部分)。在這兩種情況中的點都被標記為」已訪問「。
對於這個新集群中的第一個點,在它 ε 距離鄰域內的點已將變成相同集群中的一部分。這個讓所有在 ε 鄰域內的點都屬於相同集群的過程在之後會一直被重複做,直到所有新點都被加進集群分組中。
第 2,3 步的過程會一直重複直到集群內所有點都被確定,即所有在 ε 鄰域內的點都被訪問且被打上標籤。
一旦我們在當前集群做完這些,一個新的未被訪問的點會被提取並處理,從而會接着發現下一個集群或噪聲。這個過程反覆進行直到所有的點都被編輯為已訪問。既然在最後所有的點都被訪問,那麼每個點都被標記為屬於一個集群或者是噪聲。
基於高斯混合模型(GMM)的期望最大化(EM)聚類
k-means的一個主要缺點是它簡單地使用了集群中心的平均值。通過下面的圖片,我們可以看到為什麼這不是最好的方式。在左手邊,人眼可以很明顯地看到,有兩個半徑不同的圓形星團以相同的平均值為中心。k-means不能處理這個問題,因為不同簇的平均值非常接近。當簇不是圓形時,k均值也會失效,這也是將均值用作簇中心的後果。
 K-means不適用的case
高斯混合模型(gmms)具有更好的靈活性比K-means。使用GMMs,我們需要假設數據點是高斯分佈,相對於環形的數據而言,這個假設的嚴格程度與均值相比弱很多。這樣的話,我們有兩個參數來描述簇的形狀:均值和標準差。以二維為例,意味簇可以是任何一種橢圓形(因為我們有兩個標準差在x和y方向)。因此,每個高斯分佈會被分配到單一的聚類簇。
為了在每個聚類簇中找到這兩個高斯參數(e.g均值和標準差),我們將使用的優化算法稱為expectation–maximization(EM)。請看下面的圖片,以說明將高斯擬合聚類簇。然後,我們可以處理EM聚類過程使用gmms。
K-means不適用的case
高斯混合模型(gmms)具有更好的靈活性比K-means。使用GMMs,我們需要假設數據點是高斯分佈,相對於環形的數據而言,這個假設的嚴格程度與均值相比弱很多。這樣的話,我們有兩個參數來描述簇的形狀:均值和標準差。以二維為例,意味簇可以是任何一種橢圓形(因為我們有兩個標準差在x和y方向)。因此,每個高斯分佈會被分配到單一的聚類簇。
為了在每個聚類簇中找到這兩個高斯參數(e.g均值和標準差),我們將使用的優化算法稱為expectation–maximization(EM)。請看下面的圖片,以說明將高斯擬合聚類簇。然後,我們可以處理EM聚類過程使用gmms。
 使用GMMs的EM聚類
使用GMMs的EM聚類
-
我們首先設定聚類簇的數量(如k-means),然後隨機初始化每個集群的高斯分佈參數。我們也可以通過快速查看數據來為初始參數提供一個很好的猜測。正如上圖所示,這不是100%必要的,因為高斯操作開始時候是非常差的,但很快優化。
-
給定每個簇的高斯分佈,計算每個數據點屬於特定簇的概率。一個點越靠近高斯中心,它就越可能屬於該簇。這應該是直觀的,因為對於高斯分佈,我們假設大多數數據都靠近集群的中心。
-
基於這些概率,我們為高斯分佈計算了一組新的參數,這樣我們就可以最大化群集中數據點的概率。我們使用數據點位置的加權和計算這些新參數,其中權重是屬於特定集群的數據點的概率。為了以可視化的方式解釋這一點,我們可以查看上面的圖形,特別是以黃色集群為例。在第一次迭代中,分佈是隨機開始的,但是我們可以看到大多數黃點都在分佈的右邊。當我們計算一個由概率加權的和時,即使在中心附近有一些點,但大多數都在右邊。因此,分佈的平均值很自然地移近這些點集。我們還可以看到,大多數點是「從右上到左下」。因此,標準偏差會發生變化,以創建一個更適合這些點的橢圓,以便最大化概率加權的和。
-
第2步和第3步重複進行,直到收斂,也就是在收斂過程中,迭代變化不大。
- 我們首先設定聚類簇的數量(如k-means),然後隨機初始化每個集群的高斯分佈參數。我們也可以通過快速查看數據來為初始參數提供一個很好的猜測。正如上圖所示,這不是100%必要的,因為高斯操作開始時候是非常差的,但很快優化。
- 給定每個簇的高斯分佈,計算每個數據點屬於特定簇的概率。一個點越靠近高斯中心,它就越可能屬於該簇。這應該是直觀的,因為對於高斯分佈,我們假設大多數數據都靠近集群的中心。
- 基於這些概率,我們為高斯分佈計算了一組新的參數,這樣我們就可以最大化群集中數據點的概率。我們使用數據點位置的加權和計算這些新參數,其中權重是屬於特定集群的數據點的概率。為了以可視化的方式解釋這一點,我們可以查看上面的圖形,特別是以黃色集群為例。在第一次迭代中,分佈是隨機開始的,但是我們可以看到大多數黃點都在分佈的右邊。當我們計算一個由概率加權的和時,即使在中心附近有一些點,但大多數都在右邊。因此,分佈的平均值很自然地移近這些點集。我們還可以看到,大多數點是「從右上到左下」。因此,標準偏差會發生變化,以創建一個更適合這些點的橢圓,以便最大化概率加權的和。
- 第2步和第3步重複進行,直到收斂,也就是在收斂過程中,迭代變化不大。
凝聚層次聚類
凝聚層次聚類算法實際上分為 2 類:自上而下或自下而上。自下而上算法在一開始將每個數據點當作一個單個集群對待,然後逐步的合併(或凝聚)成對的集群,直到所有的集群被合併到一個集群中,這個集群包含所有的點。自下而上層次聚類因此被叫做層次凝聚的聚類或者 HAC。這個聚類的層次被表示為一棵樹(或者樹狀圖)。樹根是唯一的集群,他聚集了所有的樣本,葉子是只有一個樣本的集群。在接着看算法步驟之前,請查看下面的圖示說明。
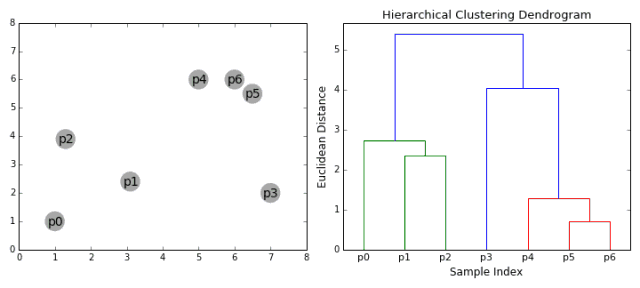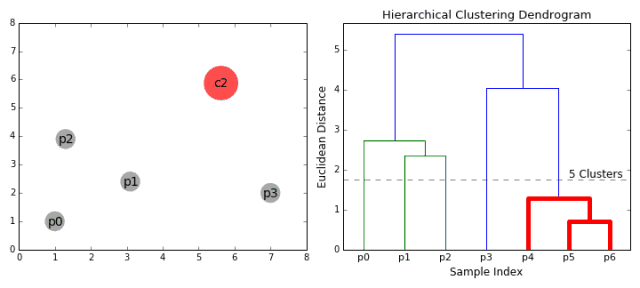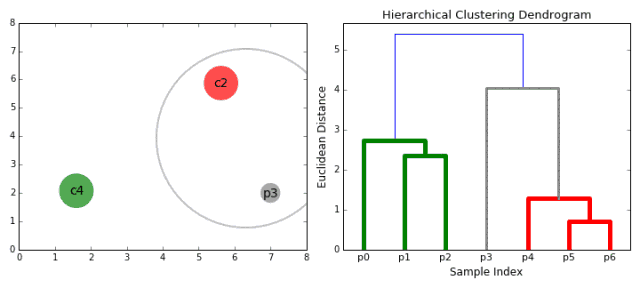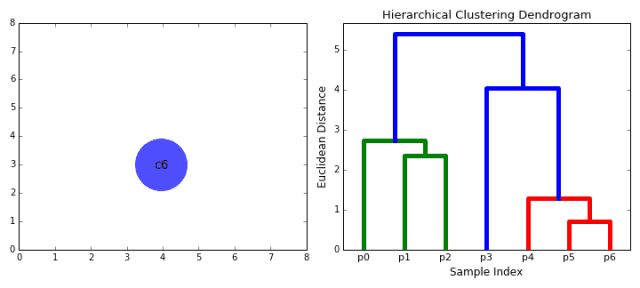 凝聚層次聚類
凝聚層次聚類
-
我們通過將每個點視作一個單個集群作為開始,即如果我們的數據集中有 X 個數據點,那麼我們就有 X 個集群。我們然後選擇一個距離度量標準來測量兩個集群之間的距離。作為一個例子,我們將用到平均連接,它將兩個集群之間的距離定義為第一個集群中的數據點與第二個集群中數據點的平均距離。
-
在每次迭代時,我們將兩個集群組合成一個。兩個將被組合的集群是在那些有最小平均連接的集群中選出來的,即根據我們選擇的距離度量標準,這些兩兩集群之間有最小的距離,且因此是最相似的也最應該被組合。
-
一直重複第二步,直到我們到達樹的根部,即我們只有一個包含所有數據點的集群。通過這種方法,我們僅僅通過選擇停止組合的集群的時機,即選擇何時停止樹的構建,就可以挑選出最終我們想要的集群數。
- 我們通過將每個點視作一個單個集群作為開始,即如果我們的數據集中有 X 個數據點,那麼我們就有 X 個集群。我們然後選擇一個距離度量標準來測量兩個集群之間的距離。作為一個例子,我們將用到平均連接,它將兩個集群之間的距離定義為第一個集群中的數據點與第二個集群中數據點的平均距離。
- 在每次迭代時,我們將兩個集群組合成一個。兩個將被組合的集群是在那些有最小平均連接的集群中選出來的,即根據我們選擇的距離度量標準,這些兩兩集群之間有最小的距離,且因此是最相似的也最應該被組合。
- 一直重複第二步,直到我們到達樹的根部,即我們只有一個包含所有數據點的集群。通過這種方法,我們僅僅通過選擇停止組合的集群的時機,即選擇何時停止樹的構建,就可以挑選出最終我們想要的集群數。